Introduction
It has become increasingly common to move away from the confidence interval procedure for elaborating election predictions and toward probabilistic measures of candidate success. Instead of calculating poll averages with margins of error, researchers calculate the probability of a certain candidate winning the election. The two procedures require the same data, however the second procedure, as argued here, yields a more palpable result (Silver 2013). Polling through random samples is supposed to offer the best information available, at operationally low cost, as to the tendency of a candidate winning an election. Nevertheless, survey data will always be accompanied by the inevitable uncertainty of sample error even when rigorously following the traditional rules of random sampling. Survey data not only represent the relative popularity of two or more candidates but also reveal options in the “do not know/refuse to answer” (dk/ref) category. The question is how the numerical results from polling should be translated into a clear statement of voter preference. We will show here that the traditional confidence interval method is a poor instrument for determining the tendencies of an election producing ambiguous results while at the same time requiring relatively large sample size. The important discussion of how probabilities should be presented for a clear and quick explanation to the public is not elaborated here. The immediate proposal is to demonstrate why one statistical method is more precise than the traditional approach. Once the probabilistic method is presented, then suggestions for the pedagogy of statistics may be produced in future work. (See Gigerenzer et al. [2007] for some interesting ideas in this area.)
A simple example
To clarify the questions asked here, we work from a simplified example shown in Table 1, using the normal approximation to the binomial for calculating confidence limits.
In Table 1, the results of a poll are presented for several sample sizes. Candidate M gets 49% of preferences from sampled voters, candidate S gets 43%, and the remaining dk/ref is 8%. Tradition in political surveys calls for the confidence level to be 95% (the acceptable minimum value for confidence), and the consequent confidence limits are reported for four different sample sizes (n = 600, 1,000, 1,067, and 2,500). For a sample size of 600, the resulting margin of error is 4%; the confidence limits for candidate M are 45% and 53% and for candidate S are 39% and 47%. In this case, confidence intervals overlap producing the ambiguous outcome that no candidate decisively leads the other at the minimally acceptable confidence level of 95%. One possible solution to the problem of overlap (and not altering the value of the confidence level) is to acquire a larger sample and consequently produce a smaller margin of error, but even with a sample size of 1,000, the margin of error would still be 3.1%, and the two confidence intervals would still share confidence limits at about 46%, once again leading to ambiguities due to overlap. As shown in Table 1, increasing the sample size to 1,067 is still not enough to eliminate the ambiguous outcome due to overlap; the LCL for candidate M equals the UCL for candidate S (46%). A popular sample size for political polling is 2,500 shown in the last columns of Table 1. This sample size is sufficiently large to avoid overlap, indicating poll results favoring candidate M in the presence of the minimally acceptable confidence level of 95%. Confidence intervals from a sample size of 2,500 may demonstrate that M is statistically preferred over S, but they do not eliminate the uncertainty of the survey outcome nor, more importantly, provide a measure of that uncertainty. This latter shortcoming is the underlying motivation for this article.
In Figure 1, the results of Table 1 are generalized for a continuum of sample sizes. Below the horizontal black line at a sample size of 1,067, the overlap of the confidence intervals indicates that the two sample means are indistinguishable at the 95% confidence level.
We propose that the impreciseness of the confidence interval can be partially overcome by asking a different question of the polling data: Given the percentage breakdown of poll results and its sample size, what is the probability that candidate M would receive more votes than candidate S, in the upcoming election. We should expect that M would win since she is apparently preferred by the electorate, but at what probability: close to certainty (probability close to 100%) or to the uncertainty of a coin toss (close to 50%). These questions will be elaborated below. We propose that the confidence interval procedure be replaced by the calculation of the probability that candidate M would receive more votes than candidate S in the election, P(Mvotes > Svotes). We will show how this calculation can be done through computer simulation.
The confidence interval does not reveal the probability that M will win the election. The confidence interval yields only limited information, that is, the likelihood defined by an interval of at least 95% confidence of getting a certain percentage of voter preferences. Therefore, 5% of the time voter preferences would be defined as relatively far from the estimate, outside the interval. In other words, 95% confidence is the complement of 5% risk. In order to eliminate overlap, the confidence level could be lowered from its traditional value of 95%, thereby making the confidence interval progressively smaller until confidence intervals become separated from one another. The cost of lower confidence levels is the greater probability of estimated preferences missing the mark. Consequently, the concept of the confidence interval can be misleading when used as strategic information in a campaign and, as we argue below, should be replaced with the probability construct that a certain candidate receives sufficient votes to win the election. We will show that the probability construct has the further advantage of requiring a smaller sample size for the same level of risk.
Simulations
With the same information used to construct the confidence interval, risk itself can be calculated through simulation in a more precise way (Samohyl 2018) and demonstrated graphically in a histogram. We can use the polling data to construct a probability model to simulate the numerical results for a large number of simulated elections (here we use 100,000), taking into account the expected deviations which occur in each simulated election due to random sampling error. An average laptop can do all 100,000 simulations in a few seconds. The outcomes of simulated elections are calculated from the multinomial distribution. The population of voters is assumed infinite; depending on certain conditions, this means in practice at least 50,000 voters. Table 2 is an illustration of the last six of the simulated values for a sample size of 600 and a total number of replications of 100,000.
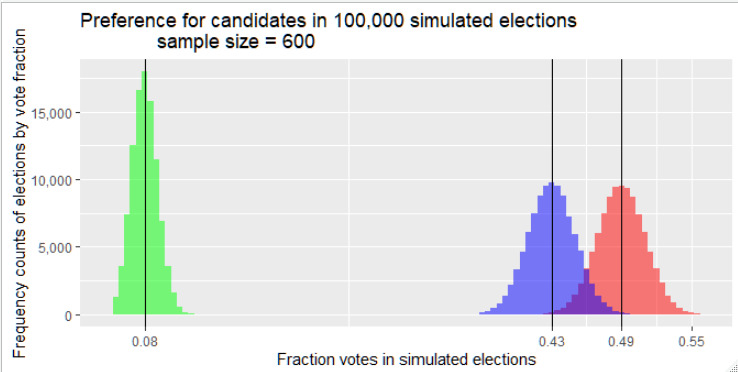
Figure 2 is constructed to show the histogram by percentage votes for M in the 100,000 simulated elections. Along the x-axis, the classification of elections is by percent of votes received by M. The vertical axis represents the frequency of the classification. As expected, the largest frequency of elections clusters around the expected value of 49%, but more importantly, due to the inherent error in random sampling, outcomes are scattered about the mean. The two vertical lines in Figure 2 separate the 95% confidence interval from the 2.5% of election returns outside the two confidence limits. Election returns that appear in these two extreme tails are called tail errors. In terms of hypothesis tests, tail errors are p-values. From the viewpoint of candidate M, an important observation is that results in the upper 2.5% tail represent little or no cost to candidate M, indicating an underestimate of voter preference represented by the mean of 49%. However, the 2.5% upper error for the confidence interval is considered just as bad as the lower error. However, upper error and lower error should be treated differently. The candidate should welcome upper error results. In other words, the upper confidence limit of 53% is a reasonable upper range for election expectations, and any value greater than this would have to be considered as an unexpected pleasant surprise. On the other side of the distribution, errors in the lower 2.5% tail represent an overestimate of preferences that would be a negative surprise for the candidate whose election performance is below the expectations of the confidence interval (confidence limit is 45%). In other words, lower tail errors come from overly optimistic polling results and possess a very high cost for the candidate in comparison with upper tail errors. The differential costs between the two tails are one of the shortcomings of the application of confidence intervals, and its correction is part of the arguments presented here.
In Figure 3, the graphical results for candidate S, and for the category dk/ref are placed alongside the histogram for candidate M. Inspection of the histograms leads to the conclusion that there exists a small probability that the election may be won by candidate S although she received less preference in the poll. However, quantifying this probability from the confidence interval is not straightforward. Even if the two histograms above are placed in the same figure, and including the histogram for dk/ref, there is no direct way of measuring the uncertainty inherent in election forecasts using confidence intervals. There can be no doubt that candidate M is the most probable winner in the election; however, after inspecting Figure 3, there are at least two ambiguities that arise. The dk/ref histogram represents voters who may or may not participate in the election, and at least some kind of assumption should be made about their preferences either deciding to vote or how their possible votes are distributed. The 8% average for dk/ref is possibly enough to invert election results. Furthermore, as the S and M histograms have shown, S is not completely dominated by M as long as there is overlap between histograms. Candidate M ranks superior to S in a strong majority of simulated elections, but a more precise measure of uncertainty, not provided from the confidence interval estimates, would be welcomed.
The probability of candidate M winning the election
In Figure 4, we illustrate the probability of M winning the election, using the results of the 100,000 simulations. Since each individual simulation is an election, we simply count the number of times candidate M receives more votes than candidate S. In this first scenario, voters who do not respond to the poll (dk/ref) do not vote in the election. In other words, there is no propagation of survey preferences from nonresponse (dk/ref) to the final vote tallies. This assumption is worthy of discussion, and relevant modifications will be proposed later. How the dk/ref behave in the election is a very sensitive part of the analysis.
In Figure 4, the demarcation of election winners is the vertical line at (Mvotes - Svotes) = 0. To the left of the vertical line, the classification count is the number of times candidate S wins in the 100,000 simulated elections, about 6,000 or 6%. The probability of M winning is 94%. Classifying and counting elections in this way eliminates the cumbersome assumption that upper tails and lower tails that define the confidence interval method should be weighted equally. As emphasized, the behavior of dk/ref will have a strong impact on the election result. In order to study this impact, we will adjust the probability of M winning with differing assumptions about the propagation of df/ref to the election.
Propagating dk/ref to the election
In each simulated election, there may be a different number of voters, considering the propagation of dk/ref (0.08) to actual voters in the election. As previously mentioned, the migration of survey nonrespondents to the election can be crucial for measuring preference. The objective here is to demonstrate the sensibility of election outcomes to the proportion and distribution of nonrespondents who eventually vote. We will see that a small swing in the preferences of nonrespondents can alter election results. In Table 3, roeM is the proportion of nonrespondents who actually vote for candidate M, and roeS is the proportion who vote for candidate S. The two proportions do not necessarily sum to 1.00 because some nonrespondents may not participate in the election.
The fifth numerical line of Table 3 reproduces the result in Figure 4. With both roeM and roeS equal to zero (no propagation), the chance of M winning the election is 93.8%. Note that this probability is the same whenever roeM and roeS are identical, at any value from zero to 50%. The practical wisdom among pollsters is that when dk/ref migrates to the election in the same proportions as the survey, then results should remain the same. This is false, as our results show. The second line shows an increase to 95% in the probability of M winning when propagation replicates the estimates of the poll (49% and 43%).
It is interesting to question at what proportions does candidate S have a better chance of winning. Table 3 shows that the chances favoring M fall below 50% when roeM falls below 13%.
Sample size, tail error and confidence
Larger samples translate into narrower confidence intervals and smaller margins of error maintaining the same confidence level (Seneta 2013). We noted this relationship in the example in Figure 1. The risk measure for candidate M, the probability that M loses the election P(Svotes > Mvotes), also diminishes as sample size increases. Continuing with the simple example from Table 1, we can show that sample size has a strong and quantifiable effect on the risk measure for candidate M. In Table 4, there are two important features: (1) the pronounced relationship between the probability measure and sample size, and (2) sample size can be relatively small and still produce rather well defined results in terms of probability. The second conclusion is especially important.
For instance, for a sample size of 2,400, which produces a margin of error of 2% at a confidence level of 95%, in the probability method the risk measure is only 0.1%. In other words, for poll results of 49% and 43% with a sample size of 2,400, there is only a very small chance of 1 in 1,000 (1 – 0.999) of S winning the election. This kind of precision is absent from the confidence interval method for the same sample size. Furthermore, even for a relatively small sample size of 1,067 used in the analysis of Table 1, the risk of M losing the election is only 2%. When this sample size is applied to the confidence interval procedure, the margin of error is 3% characterizing overlap between the two candidates and consequently no clear quantitative conclusion about the outcome of the election (see Table 1).
Furthermore, it is essential to emphasize that the probability that candidate M wins the election does not depend exclusively on the poll result that M is greater than 50% nor S is less than 50%. In the confidence interval framework, the estimates related to M and S when both are relatively proximate offers only the ambiguous conclusion of a technically tied election. Even when confidence intervals do not overlap, we are left with an ambiguous result in terms of probabilities. The probabilistic method elaborated here computes a measure of election success not present in the confidence interval method.
Conclusions
Given voters’ preferences shown through random sampling, the confidence interval method that translates preferences into intervals around averages cannot quantitatively distinguish between candidate popularity. However, the estimation of probabilities for election outcomes affords a clearer statement of election uncertainty, with the advantage of a much smaller sample size. An interesting area to pursue in the next phase of this project applies multinomial logistic regression for voter choices among multiple alternatives including candidates and other options in the dk/ref categories (Dubrow 2007; Kamakura 2016; McAllister and Studlar 1991; Nicolau 2007). In the presence of more elaborate polling results, which differentiate between income and educational levels for instance, probabilities could be further refined.
Contact information: Robert Samohyl, robert.samohyl@ufsc.br, 55-48-99608-5056, Núcleo de Normalização e Qualimetria,
Dept. Estatística,
Universidade Federal de Santa Catarina,
Florianópolis, Brazil, 88040-900