Introduction
Surveys of persons and households are implemented to answer any number of research questions and to track populations over time. Though the primary objectives of any two surveys may differ widely, they will typically feature a battery of questions relating to demographic, geographic, and socioeconomic characteristics. Responses to these questions can be used to define estimation domains, to compare or calibrate samples, and as controls for potentially confounding effects in multivariable analyses. While many of these core variables (e.g. gender, race, state, etc.) may be compared from one survey to another with little or no adjustment – through collapsing of categories, for example – income often presents a more difficult challenge. This is because household or personal income is in many cases asked in the form of categories, often as a tool to mitigate against nonresponse. The categorical nature of these questions can prove problematic, however, because the values used to define category boundaries are nonstandard and can vary from one questionnaire to another. This complicates comparisons between surveys as well as analyses that may require or benefit from a continuous income measure or different category definitions. Some examples of instances in which a continuous measure would be useful include: (1) adjusting income categories for inflation in multiyear analyses of a single data source, (2) estimation of eligibility rates for income-dependent programs such as Medicaid, (3) development of income-dependent constructs such as socioeconomic status, and (4) aggregation of individual income to higher levels such as the household or family. In instances when analytic intent and survey design are aligned, use of income categories as-collected is likely the most prudent approach, as little information would be gained from conversion to a continuous measure. Survey designers cannot always anticipate future analytic needs, however, and in these instances, having a method for conversion from categories to a continuous scale is useful. In this paper, the authors describe a method for the estimation of continuous income distributions based on existing categories as well as for interpolation between category boundaries according to estimated underlying continuous distributions.
Purpose
Ideally, in every circumstance, income responses would be provided in actual dollar amounts. Even if categories are required for a particular research purpose, it is preferable for the researcher to form the categories himself according to his own requirements. This is very often not the case, however, and researchers must deal with income data with nonideal and predetermined category boundaries [e.g. the National Crime Victimization Survey (NCVS); Truman and Langton 2014], or, in some cases, even with income data that is mixed type – both continuous and categorical (e.g. the Ohio Medicaid Assessment Survey 2015). The latter scenario is commonly encountered when survey instruments are designed to provide the opportunity for respondents to provide income ranges after initially refusing a specific dollar amount question. Regardless of the motivation for initial collection of income in categories, in many cases continuous values are required. This poses a methodological question regarding the manner in which data users should convert categorical responses to actual dollar values.
In practice, data users have some options in how to interpolate categorical income responses, though there is no clear guidance in the survey literature as to how this should be achieved. The obvious choice, and by far the simplest to implement is linear interpolation. Linear interpolation is simply a matter of randomly selecting a dollar value between a respondent’s category boundaries. This approach is attractive for ease-of-implementation but requires a strong and likely false assumption about the underlying continuous distribution. Specifically, the researcher is assuming that every value in a given category is equally probable. For narrow or central categories, an equal-probability assumption may not deviate very far from reality. For noncentral categories or for categories that are especially wide, it is much less safe to assume linearity. For example, it may not be unreasonable to assume that a respondent indicating an income value in the range of $30,000 to $35,000 was just as likely to have a true value of $30,001 as he or she was $34,999. It is much less reasonable to assume that a respondent indicating an income value in the range of $0 to $10,000 is equally likely to have a true value of $1 as he or she is $9,999. In addition to the potential for erroneously inflating lower income values through the use of linear interpolation, there is also the issue of how to address the highest category. Due to the nature of income, it is inevitable that the highest category will be unbounded to the right. With a linear approach, it is impossible to interpolate individuals in the highest category without imposing an artificial upper boundary, and doing so would introduce a similar problem encountered when interpolating the lowest category.
An alternative to an individual respondent-based linear approach is to fit a function to the cumulative densities observed at the category boundaries and to use that function to interpolate individual respondents. Using a purely empirical approach that makes no assumptions regarding the nature of the underlying continuous income distribution, one could attempt to employ polynomial interpolation based on the observed densities. This approach is unappealing in its basic form, however, in that it either precludes implementation in the highest category or makes potentially naïve assumptions about the behavior of the population in that category based solely on observed densities in lower categories. Dikhanov and Ward (2001) overcame this limitation by using a so-called quasi-exact rendering technique based on the use of fourth-order polynomials to interpolate categorical income data with the lowest and highest groups being forced to be log-normal.
The mixed-polynomial method used by Dikhanov and Ward is appealing in certain contexts in that the fitted functional form of the distribution is exact at category boundaries. In the context of a survey sample, however, this implies that sample-based percentiles are accepted without regard for potential sample variation. The authors instead seek to determine which single log-normal distribution is implied by the sample without requiring exact equality at observed boundaries. Doing so does not preclude consistency between interpolated values and observed category boundaries, though it implies that boundary percentile values must be allowed to deviate between the sample and the population. (The level of deviation is minimized by the algorithm used to estimate the distribution.) To this end, this paper describes a method for using observed boundary densities to estimate a log-normal distribution which may then be used to interpolate income categories to continuous values that are consistent with the observed category definitions. This method is not computationally intense[1] and can be easily implemented with basic software.
Methods
The following sections detail a process for estimating a log-normal income distribution based on empirical cumulative mass at category boundaries and for drawing random variates for individual respondents from that distribution that are consistent with reported income categories. The validity of this percentile-constrained inverse-cumulative density function (PCICDF) method as presented here depends on the assumption that income is log-normally-distributed. The literature shows that this assumption is reasonable – Pinkovskiy and Sala-i-Martin (2009) in particular provides a good overview of previous research efforts to validate log-normality of income, and the authors themselves show that the log-normal distribution provides superior fit to other common parametric alternatives.
Empirical Cumulative Mass at Boundary Points as Proxy
for Log-normal Percentiles
In order to estimate log-normal parameters based on a sample of categorical responses, it is first necessary to make an assumption about the nature of the categorical responses and how they relate to the underlying continuous distribution. Specifically, we assume that we are observing individuals within an ordinal classification of income and that the cumulative mass of observations at a category boundary (dollar value) is equivalent to the boundary point’s percentile value that would have been observed had the data been collected on a continuous scale. For example, if we have a five-level income variable and 63 percent of individuals indicated income values less than or in the third category ($35,000–$50,000), we are assuming that $50,000 is the 63rd percentile of the true log-normal distribution for our sample.
Minimization of Percentile Vector Distance for Estimation of Log-normal Parameters
To estimate the true underlying log-normal distribution, we choose a simple and computationally efficient algorithm based on grid-searching over a reasonable parameter space. The search grid is defined in one dimension by potential log-mean values at a specified granularity, while the other dimension is similarly defined by potential log-standard deviation values. In practice, it is important to acknowledge that a single distribution may not best represent all individuals in a given survey’s sample. The algorithm is therefore implemented across strata defined by one or more characteristics associated with income (e.g. age group, educational attainment, etc.). Our notation is defined as follows:
= The number of income categories$
= Upper bound (in dollars) for the income group, with
= Observed proportion of stratum households in income group
= Cumulative density at boundary point for stratum
= The vector of values
= Minimum potential log-mean value for candidate log-normal distributions
= Maximum potential log-mean value for candidate log-normal distributions
= Minimum potential log-standard deviation value for candidate log-normal distributions
= Maximum potential log-standard deviation value for candidate log-normal distributions
= The absolute difference between log-mean values in the set …,
= The absolute difference between log-standard deviation values in the set …,
K = The number of candidate log-normal distributions (parameter pairs) in the grid space:
= The log-mean value for candidate log-normal distribution in stratum with
= The log-standard deviation value for candidate log-normal distribution k in stratum with
= The percentile corresponding to – expressed as a proportion – for candidate log-normal distribution k in stratum h
= The vector of values pkhi
= Inverse CDF for normal distribution corresponding to candidate parameter pair k
For each candidate distribution k in a given stratum h, calculate the Euclidean distance between the vectors and as:
The final distribution k for stratum h is chosen such that the corresponding distance Ekh is minimum in the set [E1h,…, Ekh].
By estimating a log-normal distribution for income according to the method described above, we ensure that the selected distribution reflects what we know about the way income is distributed in general (it is log-normal), while allowing the distribution’s location and scale to be determined by the sample. Additionally, forgoing the requirement that a given boundary point have the same percentile value in the population distribution as observed in the sample allows for sample variation that could lead to no single log-normal distribution achieving equality at every boundary point.
Clearly, the minimum achievable distance Eh is directly related to the choice of granularity parameters δ and φ and the possibility that the true log-mean and log-standard deviation values are contained in the sets used to define the grid-space. For these reasons, it is important to leverage prior knowledge of the target population by using a reasonable range of values mkh and skh that are sure to contain the true parameters – use of auxiliary data sources can be informative here. In the absence of good starting parameters for construction of the grid-space, a two-step approach can be used. In this two-step approach, one first applies the algorithm to a wide range of parameters with low granularity. The best-fitting distribution’s parameters may then be used as central points to define narrower but more granular grid axes.
Percentile-Constrained Interpolation
Once a best-fitting distribution has been identified, random variates may be drawn from it in such a way that the resulting values lie between the boundary points bordering each respondent’s categorical response. For each respondent j in stratum h, interpolate categorical income responses to continuous values according to the distance-minimizing parameters identified in Section “Minimization of Percentile Vector Distance for Estimation of Log-normal Parameters” above as:
where
Results
In order to validate the proposed approach, three analyses were completed. The first was a simulation study that sought to determine how well the method performed at identifying log-normal parameters from categories derived from random log-normal variates. The second was a case study analysis that compared percent of the federal poverty limit (%FPL) distributions between two nationally-representative surveys where one survey reports continuous income values and the other categorical. Finally, the authors compare the PCICDF approach to common alternatives – linear interpolation and polynomial interpolation – using simulated log-normal data and derived categories.
Simulation Study
The goal of the simulation study was to establish how well the algorithm performs at identifying the correct log-normal parameters from categories when a known distribution is used to generate the categorical responses. To assess the method’s performance, two simulation parameters were introduced: (1) the number of income categories (ranging from 4 to 15 with equidistant boundaries between $0 and $100,000), and (2) the range of data-generating log-normal parameters ([m, s] pairs centered at [10.5, 1.2] and ranging ±40 percent in a common direction). Figure 1 shows the results of the simulation and is based on one million simulated data points per simulation parameter combination.
As shown in Figure 1, the algorithm estimated log-mean and log-standard deviation parameters very close to the true values. In most cases, estimated values were within 1 percent of the true values, and all others were well-controlled. Interestingly, the number of categories had very little impact on accuracy, and no impact for five or more categories.
Case Study
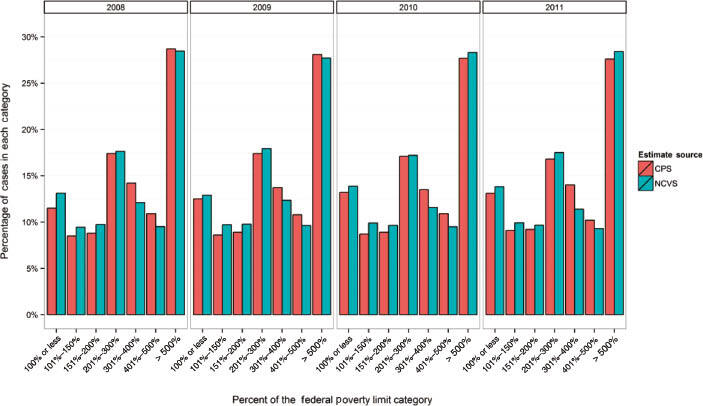
In application, the proposed method yields interpolated income values that may be used for many statistical purposes. A specific instance of application is an ongoing analysis of the NCVS conducted by the Bureau of Justice Statistics that focuses on criminal victimization among individuals across a range of %FPL categories. Since the NCVS collects income data as categories,[2] and since thresholds for the FDL change annually and do not conform to the fixed category boundaries used in the NCVS, a continuous measure of income is required. For this analysis, the method presented above was applied with strata defined as the cross-classification of householder age and race categories.[3] Respondents were then classified according to calculated percentFPL and their victimization rates compared. To validate the interpolation technique, NCVS percentFPL categories were compared to equivalently-defined categories using data from the Current Population Survey (CPS), which collects income as a continuous measure. Figure 2 shows the results of this comparison.
As shown in Figure 2, distributional agreement between the NCVS and CPS was very high, with the vast majority of estimates differing by less than 2 percentage points in any given year. Of particular note is the strong agreement of the 500 percent or greater category, as the income values used to make this classification often fall well into the uppermost income category of the NCVS which has a lower bound of $75,000. This suggests right tail estimation is performing well – an area of particular concern for income interpolation methods.
Method Comparison
Though the PCICDF method has been shown to work well on its own (both at estimating distributional parameters and matching percentFPL categories from the CPS), the previous sections have compared it with other techniques only through hypotheticals and assertion. To better understand its performance relative to common alternatives, an additional simulation-based analysis was conducted.
In order to compare methods, one million random variates were drawn from a known log-normal distribution (log-mean=10.5; log-standard deviation=1.2) and then grouped into the following eight categories: (1) $0–$9,999; (2) $10,000–$19,999; (3) $20,000–$29,999; (4) $30,000–$39,999; (5) $40,000–$49,999; (6) $50,000–$74,999; (7) $75,000–$99,999; and (8) $100,000 or more. Once grouped, the categorical data were interpolated using three methods: (1) the PCICDF method, (2) linear interpolation, and (3) fourth-order polynomial interpolation. Given the inability of the latter two methods to adequately model tail behavior in the first and last income groups, the $0–$9,999 and $100,000 or more categories were forced to be log-normal in a manner similar to that advocated by Dikhanov and Ward (2001).
Since the alternative comparison methods employ different approaches for interior and exterior categories, the following assessment addresses these groups separately. Presented first is a comparison of mean income values derived from interior categories. The second stage focuses on the potential risks of tail distribution misspecification inherent in the alternative methods. In this stage, both the overall mean and misclassification rates in alternative categories are evaluated over a gradient of log-mean misspecification magnitudes.
Restricting to interior income categories (excluding the first and last, where values are log-normal across all three analyzed methods), mean income values of $39,584, $39,516, and $40,054 were obtained from the PCICDF, polynomial, and linear interpolations, respectively. The comparison value of $39,579 obtained from the original log-normal variates shows that – for interior categories – all methods perform rather well, though the linear approach results in a slight overestimation, as expected. Among the alternatives, and all else being equal, polynomial interpolation would be preferred over a linear-based method for this reason.
Assuming that the log-normal parameters used in the first and last categories for the mixed-polynomial approach are estimated without error, the values it produces are indistinguishable on average from those resulting from PCICDF. Although, whereas estimation of log-mean and log-standard deviation values is built into the PCICDF algorithm, under the alternative approaches they must be chosen by the data user. In practice, this may prove difficult, especially for survey populations for which external income data are unavailable. If one or both parameters are poorly estimated, the overall impact could be significant. For example, when a log-mean value of 11.025 (+5 percent relative to the true value of 10.5) was used for log-normal sampling in the first and last categories for the mixed polynomial approach, the estimated overall mean income value increased by 13.7 percent. A similarly modest misspecification of 9.975 (−5 percent) in the log-mean results in an 8.9 percent reduction in the overall mean income estimate relative to the true value.
Given that a primary motivation of income interpolation for survey practitioners is alternative categorization, it is also valuable to understand what impact tail distribution misspecification has when alternative category boundaries fall in the first and last income groups. To demonstrate this impact, Figure 3 shows the percentage of cases assigned according to alternative cut-points of $5,000 and $150,000 – values that fall within the first and last categories, respectively. These percentages are shown across different levels of log-mean misspecification ranging from −10 percent to +10 percent.
As Figure 3 shows, the mixed-polynomial method is accurate when the correct log-mean is specified. It is also clear, however, that as the level of misspecification increases or decreases relative to the true value, percentage estimates take on more and more bias. Since PCICDF utilizes a single distribution for all categories, and since this distribution is estimated by the algorithm, there is no opportunity for misspecification on the part of the data user.
Discussion
Collection of income for persons or households in the form of categories is common in the design of survey instruments. Regardless of how well-founded the reasoning for such a choice, it often presents challenges for data users for whom the category boundaries are not ideal. In this paper, the authors have presented a very simple and efficient algorithm for estimating a population log-normal distribution from which the sample of categorical responses is obtained. The method has been shown through simulation to be quite accurate when the log-normal assumption holds, and case study analysis comparing nationally-representative federal surveys demonstrates that interpolated income-based estimates track well with income collected on the continuous scale. Additionally, comparison with common interpolation alternatives shows the potential downside risk of decoupling the functional forms used for interior and exterior income groups. Misspecification of tail distributions in these mixed methods can strongly impact income estimates and misclassification based on alternative cut-points. The PCICDF method does not suffer from this problem.
Though categorical values are often to be preferred – perhaps most clearly when a given measure is used to define an analysis domain, rather than as the analytic outcome of interest – it is worth noting that PCICDF can be extended to address any scenario in which ordinal categories are collected when a continuous measure is required, not just income (e.g. age categories, number of criminal victimizations, etc.). In these instances, the distributional assumptions must be revisited as necessary to suit the measure in question. Furthermore, the algorithm could be modified to address more complex scenarios when a mixture of distributions would be more appropriate. In such cases, rather than evaluating a vector of percentiles from a known function, one would obtain them empirically through simulation. This flexibility, however, would come at the expense of efficiency. Future research will address these issues as well as potential methods for measuring error in the estimation of distribution parameters.
The basic method as presented is based on a log-normal assumption – deviation from this (e.g. use of a mixture distribution with unknown quantile function) is possible through extension based on simulation at the loss of simplicity and computational efficiency.
The NCVS has 14 income categories that have fine gradations for income levels under $40,000 with ranges of $2,500 or $5,000. Income above $40,000 is split into three categories: $40,000 – $49,999; $50,000 – 74,999; and $75,000 or more.
Four categories each for race (non-Hispanic White, non-Hispanic Black, Hispanic, Other) and age (12–29, 30–49, 50–64, 65+) were used, resulting in 16 strata.