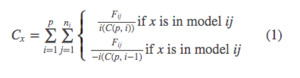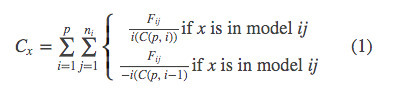Introduction
Surveys are used to measure the prevalence of a behavior or attitude in a population but also to evaluate subgroup differences in prevalence. In fact, the US Census Bureau’s website provides most measures collected cross-classified by demographic subgroup. Polls are used similarly, commonly testing for subgroup differences (e.g., Tables A1–A3 in Ramirez 2013).
Survey research also seeks to determine which subgroup prevalence differences are the most important. To determine importance, I propose that the dominance analysis (DA; see Budescu 1993; Luchman 2014) of subgroup differences offers analysts an informative, interpretable, and fair comparison between the subgroups. In the coming sections, I outline what DA is and provide an example of the advantages offered by DA by comparison to other methods using data from the General Social Survey (GSS; 1972 to 2008; Davis et al. 2010).
What is Dominance Analysis?
DA is a procedure for determining independent variable relative importance in a statistical model. DA is an ensemble method, distilling results from the collection of models representing each possible combination of independent variables in a regression analysis.
The general dominance statistic for each independent variable x (i.e., is the most common importance statistic and is computed by:
where Fij is the fit metric associated with model ij, p is the number of independent variables, ni is the number of possible combinations of size i given the p independent variables, and C(m, k) is the number of combinations of size k possible given set size m. General dominance statistics are then a weighted sum of all fit metrics in the ensemble.
General dominance statistics have several useful features for evaluating subgroup differences. First, general dominance statistics are an additive decomposition of the fit metric associated with the statistical model including all p independent variables. Therefore, the sum of all p general dominance statistics results in the value of the fit metric which includes all p independent variables. The additive decomposition property facilitates comparison between the independent variables because they are parts of a whole. If the share of the whole associated with independent variable x is greater than the share associated with independent variable y, then independent variable x is more important than independent variable y.
Second, general dominance statistics account for covariation between the independent variables, yet are not dependent on a single statistical model. As an ensemble statistic, a general dominance statistic incorporates all fit statistics associated with independent variable x, yet also adjusts the sum for models which do not include independent variable x (i.e., the bottom summand of Equation 1). The adjustment makes the general dominance statistic reflect the average marginal or incremental contribution independent variable x makes to the fit metric across all potential kinds of overlap with other independent variables. Thus, general dominance statistics allow for an evenly balanced comparison of the independent variables.
Finally, general dominance statistics can also encompass several individual coefficients or statistics simultaneously. To be specific, DA can group together a subgroup/independent variable’s dummy codes and require that all of a subgroup’s dummy codes be considered an inseparable set in the ensemble of models. Thus, the fit metric associated with the entire set of dummy codes for a subgrouping is incorporated into a single value facilitating interpretation by efficiently summarizing the total impact of all the subgroup differences.
Illustration of Dominance Analysis for Subgroup Differences
To demonstrate how DA can facilitate determining which subgrouping is most important, I use data from the GSS’ 1978–2008 cumulative file (Davis, Smith, and Marsden 2009) focusing on evaluating subgroup differences in the survey measure PARTYID, which represents respondents’ political party affiliation and strength with on a 7-point scale with the following options: strongly democratic (coded 1); not strong democrat; democratic, near independent; independent; republican, near independent; not strong republican; and strong republican (coded 7).
The subgrouping variables chosen to evaluate differences on political party affiliation were 1) SRCBELT representing urbanicity or the kind of urban area in which the respondent lives with the following categories: not assigned, largest 12 SMSAs, 13-100 largest SMSAs, largest 12 suburbs, 13-100 largest suburbs, other urban, and other rural, where SMSA means metropolitan statistical area as designated by the US Census Bureau. 2) WRKSTAT or the respondent’s current employment status with the following categories: full-time, part-time, temporarily unemployed, laid off, retired, attending school, keeping house, and other. 3) MARITAL or the respondent’s current marital status with the following categories: married, widowed, separated, divorced, and never married. 4) SEX or the respondent’s biological sex with male and female options. All don’t know, not applicable, and no answer responses were treated as missing and list-wise deleted from the dataset.
Using the four subgrouping variables and the political party affiliation measure, arguably the most straightforward method for attempting to determine which subgrouping is most important would be to cross-classify all four subgrouping variables with the survey measure separately. The cross-classification approach has obvious drawbacks in that it requires the analyst to compute and interpret the output from four tables of values encompassing a total of 154 separate proportions (e.g., 7*[7+8+5+2] to represent all levels of the survey response and subgroupings).
As opposed to evaluating all 154 proportions, a more interpretable index of importance can be obtained from the cross-classifications using the methods outlined by Goodman and Kruskal (1954). As applied to the GSS data, the strongest Cramér V statistic (e.g., 1946) was obtained by biological sex (0.0801), followed by marital status (0.0748), then urbanicity (0.0608), and finally employment status (0.0582). The cross-classification methods produce a clear hierarchy among the subgroupings, which facilitates interpretation, showing that biological sex is the most important. A shortcoming of the cross-classification methods is that the subgrouping with the strongest association with the survey measure (i.e., biological sex), irrespective of overlap/confounding with other subgroupings, will be chosen as the most important.
One way to ensure the comparison between the subgroupings is fairer in terms of adjustment for subgrouping overlap is to force them to compete in a statistical model to predict the survey measure. Because the political party affiliation measure can be represented as an ordered measure of liberality (low scores) to conservatism (high scores), political party affiliation was regressed onto all the subgroups as sets of indicator variables in an ordered logistic regression. The result from the regression is displayed in Table 1 in their more interpretable odds ratio (OR) form. All effects are compared to the first group as described above (i.e., not assigned, full-time, married, and male).
All four subgroupings show at least a few ORs associated with dummy codes that move away from the null effect of 1. Thus, ORs much lower than 1 show tendencies for the focal group to respond as being more politically liberal than the comparison group and ORs much more than 1 show tendencies for the focal group to respond as being more politically conservative. Table 1 thus reveals that urbanicity as well as marital status have the most substantial individual effects (e.g., Largest 12 SMSAs=0.5508; Divorced=0.6771) which are accompanied by several other effects of somewhat smaller size. Given the results in Table 1, it seems that either urbanicity or marital status is the most important subgrouping, and it is possible that they are in a close race for most important. By contrast, biological sex and employment status both appear to be less important as both have smaller effects and, similarly, it is possible that they are both in the running for either 3rd or 4th rank.
Whereas the ORs provide some direction for understanding how important each of the subgroupings are, the ORs provide evidence that is inconclusive as it is not clear which combination of ORs is more substantial than the others. Moreover, the ordered logistic regression is dependent on the results from the model with all the subgroupings simultaneously. Thus, strong relationships between the subgroupings could strongly affect the results and have produced results that are substantially different than those obtained using the cross-classification.
As was discussed above, DA incorporates the results of all possible combinations of models, therefore balancing predictive usefulness across models with many and few subgroupings/independent variables. The DA results uses the methodology offered by Luchman (2014) for ordered logistic regression with each subgrouping’s dummy codes grouped together as a single independent variable in the DA. The DA adds to the ordered logistic regression results in Table 1 by displaying both the value of the McFadden pseudo-R2 which has been ascribed to each set of subgroup indicators as well as the rank order of the subgroup indicators based on each independent variables’ ascribed share of the R2.
The primary advantage of the DA results over the ordered logistic regression’s ORs deals with the clear hierarchy it generated for the subgroupings. In line with the ordered logistic regression results, urbanicity and marital status emerged as the top two subgroupings, and biological sex and employment status emerged as the bottom two subgroupings. The dominance analysis shows, however, that the share of the R2 ascribed to urbanicity is well over 50 percent (i.e., 0.0046/0.0073=63%), a substantial margin of dominance over marital status, which obtained a value near 20 percent. Thus, contrary to the intuition offered by the ordered logistic regression alone, in which the degree of difference was less clear, the urbanicity subgrouping is clearly most important and is shown to be ~3 times more important than marital status; primarily due to Urbanicity’s smaller overlap with other subgroupings. Additionally, the degree of difference between biological sex and employment status in terms of their ascribed percentage of the R2 is very narrow – which is not obvious from the ordered logistic regression’s ORs alone.
In sum, the DA results effectively distill the myriad ORs obtained in the full ordered logistic regression model along all other models including different combinations of subgroupings. Moreover, the DA results produced a single, simple to interpret value to represent the importance of each subgrouping.
Weighted Dominance Analysis
Although useful for identifying important subgroup differences, one drawback to DA is it assumes the data were collected using simple random sampling (i.e., no model misspecification in terms of design; Azen and Traxel 2009; Luchman 2014). How to validly compute dominance statistics with complex sampled data has not been addressed in the literature. Because most nationally representative polls and surveys (such as the GSS) use complex sampling designs, the question of how to incorporate complex sampling design information into DA is necessary for unbiased subgrouping comparisons.
The approach I recommend for unbiased dominance statistics from complex sampled data is to a) use a log-likelihood-based model fit index, and b) to use weighted regression analyses to compute the dominance statistics.
DA is primarily a descriptive procedure that is focused on evaluating the contributions to model fit made by the subgroup’s indicators (Grömping 2007). Thus, dominance statistics will be driven only by the values of the point/coefficient estimates from the regressions. As a consequence, the pseudo-log-likelihood (sum of the products of observation-level weights and log-likelihoods) used by complex sample-adjusted data can be used just as a log-likelihood for computing a pseudo-R2 such as the McFadden’s pseudo-R2 (1973) recommended in previous research. Whereas the pseudo-log-likelihood alone can underestimate the variability/standard error of the parameter estimates, the pseudo-log-likelihood is sufficient to estimate parameters (see Roberts et al. 1987). Thus, the pseudo-log-likelihoods can be used to replace traditional log-likelihoods for the purpose of obtaining a pseudo-R2.
In addition, because most other aspects of complex sampling designs (i.e., strata indicators, clustering), only affect estimates’ sampling variability and not the parameter estimates, only survey weights are needed to obtain unbiased dominance statistics (e.g., Roberts et al. 1987).
To demonstrate the non-trivial adjustment survey weights can have on DA results, I re-conducted the DA in Table 1 with the GSS’ survey weight applied to all years in the sample (i.e., the WTSSALL weight). Table 1 reveals that biological sex and employment status actually reversed in rank order due to the effect of the survey weights, resulting in employment status being more important than biological sex (though the estimates were identical when rounded to four significant digits). Whereas the above demonstration shows that weights can affect subgrouping importance, the next section offers stronger evidence of the increase in accuracy that can be attained by weights under complex sampling designs using a simulation. Specifically, the simulation was conducted to demonstrate that in complex sampling situations, using survey weights alone can recover unbiased dominance statistics.
Methods
Simulations were conducted using Stata 12.1 (StataCorp 2011). A population of size 30,000 was simulated representing three strata of size 10,000. Five variables were simulated (a binary survey measure and four binary subgroup indicators) that were based on the population correlation matrix used by Azen and Traxel (2009, table 4) . In order for the weights to provide information about the estimates, the different strata were given different patterns of inter-correlations. Specifically, stratum 1 had a pattern of relationships that matched those from Azen and Traxel. Stratum 2 had a pattern of relationships that were uniformly 0.1 less than those from Azen and Traxel (i.e., instead of 0.7, the X1Y correlation was 0.6). Finally, stratum 3 had a pattern of relationships that were ½ the magnitude of those from Azen and Traxel (i.e., instead of 0.7, the X1Y correlation was 0.35). All variables were generated to be distributed unit multivariate normal (means 0, SDs 1), and discretized by splitting at 0; all scores above 0 were coded as 1, the rest were coded as 0.
The strata were unequally sampled from to simulate a complex sampling design. Specifically, the proportion sampled from each stratum was obtained by using the probability density from a Beta(2, 1) distribution, which produces a negatively skewed distribution with values that range between 0 and 1. The probability density between values 0 and 0.33, or ~58 percent of the sample, was assigned to be sampled from stratum 1. The probability density between values 0.33 and 0.67, or ~24 percent of the sample, was assigned to be sampled from stratum 2. The probability density between values 0.67 and 1, or ~18 percent of the sample, was assigned to be sampled from stratum 3. One thousand population members total were then randomly sampled within each stratum from the population of 30,000 using the sampling fraction designated for each stratum (~580 from stratum 1, ~240 from stratum 2, ~180 from stratum 3). Survey weights for each stratum were generated as the inverse sampling fraction from the population in their stratum for each sample member.
A DA was then conducted on the sampled cases predicting the survey measure using the subgroup indicators with and without weights and stratification (four conditions total). A fifth comparison condition where 1,000 cases were obtained as a simple random sample from the same population of 30,000 was also obtained. The DA was based on probit regression-based McFadden’s R2s and the Stata program domin (Luchman 2013). One thousand repetitions of the simulation were conducted.
Results
Table 2 shows that the survey weights recover the population values in the stratified sampling situation. In fact, the weighted DA (“Weighted-only” and “Stratified and Weighted” columns) are very similar to those obtained from the population as well as those based on simple random sampling (i.e., the “Simple Random Sample” column). Consistent with my assertion above that complex survey features other than survey weights are not useful for importance determination, incorporating strata into the regressions used in the DA was irrelevant to dominance statistic computation, producing no change from the (un-)weighed results (i.e., compare “Unweighted” to “Stratified-only” and “Weighted-only” to “Stratified and Weighted” columns).
The central conclusion to be drawn from the simulation is that unweighted and stratified-only analyses tend to produce values that are inaccurate because they overemphasize the contribution of overrepresented strata and underemphasize the contribution of the underrepresented strata relative to the population. In contradistinction, analyses that incorporate the survey weights properly calibrate the sample representation by stratum and result in more accurate dominance statistics.
Recommendations and Discussion
DA is usually considered a supplement to and not a replacement for a regression analysis (e.g., Nimon and Oswald 2013). Whereas DA supplements regression, I have shown that dominance statistics can be much more interpretable than regression coefficients for determining subgroup importance.
The simulation above also shows that in situations where survey weights are required, using a likelihood-based fit metric and the survey weights alone produces unbiased dominance statistics and is the recommended method to make the importance determination sampling design-unbiased – a situation that can result in the rank order of importance of subgroupings to change as was observed in the GSS, political party affiliation example.
When to Use Dominance Analysis
DA is recommended when the survey measure and subgroupings meet several criteria, specifically:
- There are multiple, partially overlapping subgroupings;
- The survey measure lacks an easily interpretable metric;
- There are many categories within the subgrouping(s).
The DA method provides a theory-grounded method for ascribing components of a fit metric to multiple, correlated independent variables. Thus, when subgroupings overlap, the DA method provides a useful, fair way to determine which is most important. Situations where the subgroupings are independent provide less benefit to interpretation.
The DA method provides a relative metric by which to determine importance based on the focal fit metric, which can avoid the arbitrariness of most survey questions’ scales. By contrast, meaningful survey metrics could be better analyzed using regression analysis’ results. Finally, the DA method allows for grouping and representing the effect of several regression coefficients simultaneously, which can greatly facilitate interpretation.
The political party affiliation example from the GSS meets all three desirable criteria for DA and was a critical tool for determining importance.