Introduction
The use of surveys remains one of the most popular research methodologies for graduate studies and published papers. With so many research studies utilizing survey research methods, it is increasingly important that survey instruments are functioning the way they are intended and measuring what they claim. The quality of the instrument used in the measurement process plays a fundamental role in the analysis of the data collected from it. It is important to begin at the level of measurement and to identify weaknesses that may limit the reliability and validity of the measures made with the survey instrument (Bond and Fox 2001).
This study utilizes the Rasch model to assess the quality of an instrument and structure of the rating scale. Specifically, this study examines the inclusion, or exclusion, of a neutral middle category for Likert-type survey responses. This middle category can have many different titles such as “neutral,” “not sure,” or “neither.” The meaning of this category is often unclear, and researchers have hypothesized that respondents may be interpreting this category in a variety of different ways.
Rationale and Background
Many surveys include a neutral middle category as a way to make respondents feel comfortable; however, by allowing the respondent to be noncommittal and choose a response that is located in the middle of a scale, the specificity of measurement is being diminished or even washed away. In an effort to create a survey instrument that provides maximum comfort to the respondent, instrument developers are compromising their own data collection by allowing for a situation in which information is lost and/or distorted.
When employing a “neutral” or “unsure” response option on a survey, researchers should be mindful that this scale construction could have major implications on their survey data (Ghorpade and Lackritz 1986). Selecting a neutral response option can be interpreted by researchers to suggest varying intents by the survey respondent. Choosing the “neutral” response may be interpreted as the midpoint between two scale anchors, such as a positive and a negative (Ghorpade and Lackritz 1986). Selecting the “neutral” response option could also represent that the respondent was not familiar with the question or topic at hand and, as a result, was not sure how to answer this particular item (DeMars and Erwin 2004). Furthermore, the “neutral” response option may indicate that the respondent does not have an opinion to report or that he or she is simply not interested in the topic (DeMars and Erwin 2004). Research has shown that the presence of a “no opinion” or “don’t know” option reduces the overall number of respondents that offer opinions (Schaeffer and Presser 2003).
While respondents may view response categories of “neutral,” “not sure,” and “no opinion” to be one in the same, these options are, in fact, dissimilar, and these response categories should be used with intention. Researchers apply the “neutral” category to indicate that a respondent is declaring the middle position between two points while “no opinion” or “don’t know” are intended to reflect a lack of opinion or attitude toward a statement (DeMars and Erwin 2004). A further response option used as a middle category in survey research is “unsure” or “undecided.” These options are intended to be used as an option when a respondent is having difficulty selecting between the other available responses (DeMars and Erwin 2004).
Even though these neutral response categories are frequently used on surveys, how these responses should be scored is largely undetermined (DeMars and Erwin 2004). Neutral response options do not affect all surveys equally, and therefore, a single method for working with neutral response options is not generalizable as researchers need to consider the survey construct (DeMars and Erwin 2004). Researchers utilizing a neutral middle category must make a conscious decision regarding how these responses will be scored. In survey research, using neutral response options are often manipulated in an overly simplistic manner (Ghorpade and Lackritz 1986).
Rasch vs. Classical Test Theory Approach
When attempting to construct measures from survey data, the classical test theory model (sometimes called the true score model) has several deficiencies. The classical test theory approach requires complete records to make comparisons of items on the survey. Even if a complete scoring record is attained, the issue of sample-dependence between estimates of an item’s difficulty to endorse and a respondent’s willingness to endorse surfaces. Moreover, the estimates of item difficulty cannot be directly compared unless the estimates come from the same sample or assumptions are made about the comparability of the samples. Another concern with the classical test theory approach is that a single standard error of measurement is produced for the composite of the ratings or scores. Finally, there is a raw score bias in the classical test model in favor of central scores and against extreme scores, meaning that raw scores are always target-biased and sample-dependent (Wright 1997).
The Rasch model, introduced by Georg Rasch (1960), addresses many of the weaknesses of the classical test theory approach. It yields a more comprehensive and informative picture of the construct under measurement as well as the respondents on that measure. Specific to rating scale data, the Rasch model allows for the connection of observations of respondents and items in a way that indicates a person endorsing a more extreme statement should also endorse all less extreme statements, and an easy-to-endorse item is always expected to be rated higher by any respondent (Wright and Masters 1982). Information about the structure of the rating scale and the degree to which each item contributes to the construct is also produced. The model provides a mathematically sound alternative to traditional approaches of survey data analysis (Wright 1997).
Physical placement of a “neutral,” “no opinion,” or “not sure” response category can have implications for the respondent as well as the analysis of survey responses. A scale that reads “strongly disagree-disagree-agree-strongly agree” is assumed to increase with each step of the scale, agreeing with the item more and more. However, when a response such as “neutral” or “not sure” is inserted into the middle of the scale between disagree and agree, it can no longer be assumed that the categories are arranged in a predetermined ascending or descending order. The interpretation of a middle category in a Likert-type survey scale can also be problematic. What does it mean for a respondent to select “not sure,” “neutral,” or “neither” on an item that the respondent should, and probably does, have an opinion about? The answer to this question can have a profound impact on the analysis of the responses.
Here, the issue of whether or not to include a middle category, as well as placement of the middle category, for Likert-type survey instruments is examined. This study has practical and methodological implications. It serves as an assessment of the survey itself by ensuring the survey is functioning as it was intended. It can also benefit survey developers by giving insight into possible revisions for future rounds of data collection. Methodologically, this study serves as a framework for educational researchers developing survey instruments and analyzing rating scale data.
Methods
Instrumentation
This study utilizes the Rasch model to assess the measurement instrument and the structure of the measurement scale of a typical data set collected in higher education settings. The survey instrument asked respondents to indicate their level of agreement or disagreement with a series of 13 statements related to academic readiness. The statements were adapted from existing scales on the topics of student self-efficacy and procrastination, both of which are shown to be indicators of student college readiness in existing literature. This instrument utilized a five-point rating scale: 1=Strongly Disagree, 2=Disagree, 3=Not Sure, 4=Agree, 5=Strongly Agree.
Data Set
The response frame included responses from 1,665 first-year students at a large research university in the southeast United States. The Office of Institutional Effectiveness sent out a broadcast email with an imbedded web-survey link to all first-year students (as determined by the University Registrar) who were enrolled at the university in the fall semester. Students were informed that although student identification numbers were collected, all responses would be aggregated with the goal of confidentially.
Analysis
Georg Rasch (1960) described a dichotomous measurement model to analyze test scores. Likert-type survey responses, such as those in this study, may be analyzed using a rating scale model; an extension of Rasch’s original dichotomous model designed to analyze ordered response categorical data (Andrich 1978; Wright and Stone 1979) shown here as:
\[ln \bigg(\frac{P_{nij}}{Pni(j-1)}\bigg)=Bn -Di -Fj\]
Where Pnij is the probability that person n encountering item i would be observed in category j; Pni(j–1) is the probability that the observation would be in category j–1; Bn is the “ability” of person n; Di is the difficulty of item i; and Fj is the point where categories j–1 and j are equally probable relative to the measure of the item.
A Rasch model was employed, because it uses the sum of the item ratings simply as a starting point for estimating probabilities of those responding. Item difficulty is considered the main characteristic influencing responses, and it is based on the ability to endorse a set of items and the difficulty of a set of items. In general, people are more likely to endorse easy-to-endorse items than those that are difficult to endorse. People with higher willingness-to-endorse scores are more agreeable than those with low scores.
A rating scale model was applied to test the overall data fit to the model by using the software package, WINSTEPS version 3.51 (Linacre 2004). Missing data were treated as missing, as the Rasch model has the ability to deal with such entries without imputing estimates or deleting any portion of the data. There were 1,595 respondents measured on the 13 items for this survey.
This study utilizes three separate models for analysis. The first is simply the original rating scale with the middle category “3=Not Sure” For the second analysis, the response category “3=Not Sure” was recoded as missing and the model was re-run. The final analysis entailed moving the “3=Not Sure” category to the end of the scale and running the model again. These analyses provided for three scenarios: (1) the original 5-point scale, (2) a 4-point scale with the middle category removed, and (3) a 5-point scale where “not sure” has moved to the end of the rating scale.
Results and Discussion
Category Probabilities
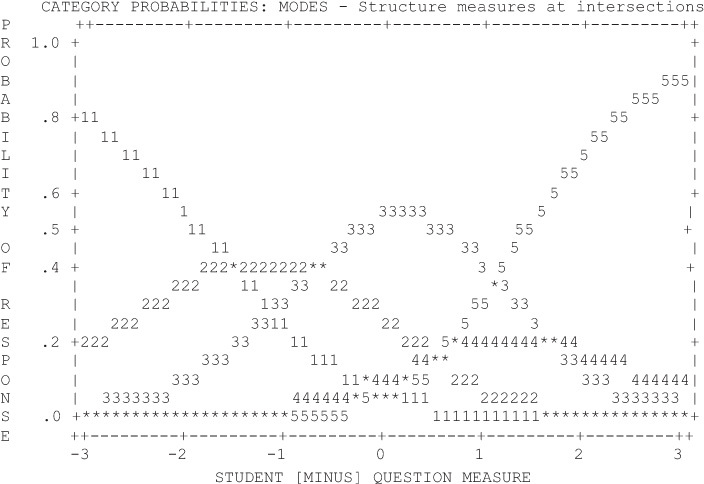
To investigate measurement flaws related to the middle category, a logical place to begin the discussion is to inspect the fit and function of the rating scale itself. Table 1 shows the observed average measures of the rating scale for each rating category based on where the middle category “not sure” option was placed along the scale. The average observed measures should increase monotonically as the rating scale increases, and at some point along the continuum, each category should be the most probable, as shown by a distinct peak on the category probability curve graphs (Linacre 2002).
The category probability curves are shown as Figures 1–3. The x-axis represents what is being measured, here academic readiness, as defined by the questions on the survey under analysis. The y-axis represents the probability of responding to any category, ranging from 0 to 1. For example, looking at category 1 (1=Strongly Disagree), the likelihood of a person responding strongly disagree decreases as their level of preparedness increases. Theoretically, each response category should peak at some point on the graph.
Figure 1 represents the categories as originally coded, with “not sure” in the middle. Figure 2 coded “not sure” as missing, and Figure 3 placed “not sure” at the end of the scale. These figures indicate that the only case in which each category clearly had a peak where it was the most probable response was with “not sure” coded as missing (Figure 2). Thus, the model that lacks a middle category is preferred from a measurement perspective.
Item Hierarchy
The item hierarchy, which can also be viewed as the endorsability of the survey items along a continuum of easy-to-endorse to hard-to-endorse, is also an important aspect to consider when inspecting the impact of a middle category. Table 2 shows the item estimates for each item based on where the middle category “not sure” option was placed along the scale. The average item measure is preset to zero. Items with positive estimates are harder to endorse while items with a negative estimate are easier to endorse. These item estimates are illustrated visually for each rating scale model in Figures 4–6. A change in the order of items along the continuum would indicate the construct being measured, here academic readiness, is affected by the inclusion or displacement of the middle category.
Figures 4 and 5 show a similar spread of items along the continuum, indicating a similar measurement construct when “not sure” is in the middle as well as coded as missing. Figure 6, when “not sure” is moved to the end of the scale, exhibits a very narrow range of scores for both items and people. Figure 5 exhibits the best spread of both people and items along the continuum, which is preferable from a measurement point of view.
Conclusion
This study provides a demonstration showing that, for constructing measures from survey responses, the inclusion of a neutral middle category distorts the data to the point where it is not possible to construct meaningful measures. As noted by Sampson and Bradley (2003), the classical test theory model produces a descriptive summary based on statistical analysis, but it is limited if not absent of the capability to assess the quality of the instrument. It is important to begin at the level of measurement and to identify weaknesses that may limit the reliability and validity of the measures made with the instrument. As indicated in the study, Rasch analysis tackles many of the deficiencies of the classical test theory model in that it has the capacity to incorporate missing data, produces validity and reliability measures for person measures and item calibrations, measures persons and items on the same metric, and is sample-free.
Some may presume that respondents have an accurate perception of the construct, rate items according to reproducible criteria, and accurately record their ratings within uniformly spaced levels. However, survey responses are typically based on fluctuating personal criteria and are not always interpreted as intended or recorded correctly. Furthermore, surveys utilizing Likert-type rating scales produce ordinal responses, which are not the same as producing measures (Wright 1997). Rasch analysis produces measures, provides a basis for insight into the quality of the measurement tool, and provides information to allow for systematic diagnosis of item fit. This study illustrates and highlights many issues with the inclusion and placement of a middle category through a measurement lens.