The Youth Tobacco Survey (YTS) was developed in 1998 by the Centers for Disease Control and Prevention, Office on Smoking and Health (OSH) to provide states with data needed to design, implement, and evaluate comprehensive tobacco control programs. The YTS is a school-based survey of adolescents in grades 6 through 12 usually conducted only in public schools but also in private schools when a state elects to do so. State departments of health field the YTS during the fall or spring term of an academic year at their discretion.
Examining correlates and trends in response rates is important since response rates are often used as a measure of survey quality. We could not locate any studies that have examined seasonal variation in response rates to self-administered, school-based surveys. To test the hypothesis that the fall is more favorable for increasing response rates to school-based surveys than the spring, we included YTS surveys conducted from 2000–2008. The word ‘season’ is equivalent to ‘term’ in our analysis, and we use the two words interchangeably.
Methods
Sample
The YTS uses a two-stage sample design in which schools are randomly selected with probability proportional to enrollment size. Classrooms are chosen systematically within selected schools, and all students in selected classes are eligible to participate. Schools that decline to participate are not replaced, and substitutions for schools or classes are not allowed. Thus, the methodology used to select schools and classrooms is identical both in the spring and fall terms.
All surveys (2000–2008) were conducted in the fall or spring of each academic year and included middle, junior high, and high school students from public and some private schools. Grades were divided into two classifications: middle (grades 6 through 8) and high school (grades 9 through 12). Forty-two states that had conducted a YTS during these years plus the District of Columbia and Puerto Rico granted us permission to use their data for our analyses.
Statistical methods
The overall response rate for each survey is the product of the two response rates resulting from the stages of sample selection – school and student. We will not examine the overall rate, but instead will look separately at the school and student response rates since they have different correlates. The school response rate is influenced primarily by the factors that produce refusals in individual level surveys. Schools must be convinced to participate in the survey, and they have a myriad of reasons for not doing so, primarily disruption of the school schedule and loss of teaching hours. These reasons in turn are affected by demographic and societal factors, such as in which region of the country the school is located and how many class periods must be devoted to the testing required by state and federal law. On the other hand, student response rates are largely a function of attendance levels and the strictness of the parental permission procedure.
School and student response rates were calculated for each of the forty-four states or territories by year and term, covering a total of 309 surveys and about 858,070 students. The school response rate was derived by dividing the number of participating schools by the number of selected schools and the student response rate by dividing the number of participating students by the number of eligible students. Statistical analyses were conducted using SAS version 9.2 (SAS Institute Inc., Cary, NC) software.
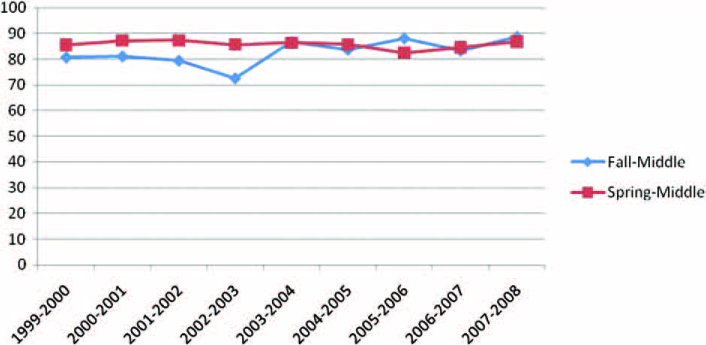
We calculated basic descriptive statistics (means, confidence intervals, and average differences). Independent sample two-sided t-tests were then calculated to determine if the fall and spring response rates differed significantly at p≤0.05. To determine whether or not there are any substantial patterns over time that may have cancelled each other out in the basic descriptive analysis, we graphed the means by year and season for each type of response rate at each school level.
We go beyond bivariate analysis and test for seasonal effects in a multivariate context controlling for other factors that might influence response rates. In this way, we are able to take into account changes over time. Separate ordinary least squares (OLS) regression models were calculated for the two rates. The primary independent variable of interest for the analysis was season (fall or spring). Of the additional independent variables that may have influenced differences in response rates, we included school level (middle or high), calendar year the YTS was conducted (to make the constant an interpretable statistic, we coded the calendar year as 2000=0, 2001=1 … 2008=8.), experience in conducting YTS surveys, region of the country, the percentage of the state population living in urban areas as of the 2000 U.S. Census, and the percentage of both African Americans and Hispanics in the state’s total middle and high school enrollments. Experience conducting a YTS was based on a points system. States that conducted both a middle school and high school YTS in a calendar year were given 1 point. States that conducted a middle school-only YTS or high school-only YTS in a calendar year were given 0.5 point. We use this half point scheme because the middle and high school surveys are entirely separate surveys requiring different methods for achieving high response rates. When a state decides to conduct only one of the pair, it has in essence completed half the work. Points were cumulative across all survey years (2000–2008). Region was coded into four categories according to U.S. Census definitions. The percentages of enrolled students who were African American or Hispanic came either from the weighted data files or from the actual state percentages provided by the state departments of education. The percent urban was taken from the U.S. Census Bureau, 2000 Census of Population and Housing, Population and Housing Unit Counts PHC-3. Since almost all surveys included in this study employed passive, rather than active, parental permission, we must consider that this factor had no effects on our results.
Results
A separate prior analysis of YTS data from 2006 had suggested average overall high school response rates may be slightly higher in the fall term than in the spring. This led to the more general hypothesis that response rates to school-based surveys conducted in the fall at either level will be higher than in surveys conducted during the spring. Table 1 displays the basic descriptive statistics for school and student response rates by level and the term in which the survey was conducted. Regardless of type of response rate, only small differences between the terms were observed and none were statistically significant at a p-value ≤0.05.
The higher number of surveys conducted during the spring versus the fall, reflected in Table 1, suggests that state administrators, who schedule the YTS, prefer the spring term despite the usually crowded calendar at the end of the school year. There is, however, a methodological reason why more states choose the spring term. Enrollment data upon which the sample must be based usually are not available before the end of October. This leaves almost no time to collect data for even a very small YTS (less than one thousand respondents). Thus the spring term is more advantageous for drawing an up-to-date sample and for carrying out the fifteen hundred surveys that characterize a typical YTS.
Figures 1–4 display the year-to-year percentages by response rate and season. Only the series of school response rates for high schools reveal that spring surveys have slightly higher response rates than fall surveys – the opposite of our hypothesis. The time series for the student rate does not show much variation at either level largely because almost all students in participating classes are respondents. Under the passive consent procedure, the student response rate closely tracks the class attendance rate. As a result, the school response rate drives the overall rate. In the past, lax substitution of classes willing to participate for those unwilling contributed to the high student response rates. Current strict monitoring of the class selection process is likely to lower student response rates and increase their variation beginning in 2009. As a result, the contribution of the student response rate to the overall rate may increase.
Controlling for several confounding factors in regression analyses does not change our previous findings about the effect of season. None of the coefficients for fall term, displayed in Table 2, indicate a significant effect of season (fall or spring) on any of the response rates. Among the other independent variables included in the analysis, school level had a large negative impact on response rates with high schools having lower student (p≤0.001) response rates than middle schools. Region of the country also affected participation, usually significantly. Except for the student response rate in the West, the regions uniformly had positive effects suggesting rates were higher in these regions than in the South. Hispanic origin and greater urbanicity tended to decrease one or both of the response rates.
Conclusion
Our study results do not support the hypothesis that conducting the survey during the fall season significantly increases YTS response rates, and the multivariate analysis confirms the bivariate results of no difference as shown in Table 1. Scheduling a survey during the fall compared to the spring makes no difference in participation regardless of school level (i.e., middle or high). Of the other independent variables we evaluated, middle schools outside the South with lower proportions of Hispanic students were most conducive to producing high response rates. However, our explanatory model explains only a small fraction of the variance in each response rate. Identifying additional factors that may affect response rates would provide more substantive evidence to states on how to increase participation in the YTS and would be a useful topic for future operational research.
Our findings contribute to the ongoing discussion of how to maintain and increase response rates in self-administered surveys among adolescents. Shifting data collection from the spring to the fall is not a strategy likely to increase response rates consistently. More importantly, we have also demonstrated that response rates have not declined over time. YTS surveys, on average, have exceeded and continue to exceed the YTS response rate standard of 60.0%. Careful monitoring of response rates will be a continuing effort in the administration of the YTS so that the factors that impact them significantly can be located.